최소 신장 트리(MST : Minunum Spanning Tree)
신장 트리(Spanning Tree) 중에서 사용된 간선들의 가중치 합이 최소인 트리
신장 트리(Spanning Tree)
n개의 정점으로 이루어진 무향 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리
그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않은 부분 그래프

정점이 N개인 무방향 그래프에서 나올 수 있는 최대 간선의 수 : N(N-1)/2
정점이 N개인 방향 그래프에서 나올 수 있는 최대 간선의 수 : N(N-1)
크루스칼 알고리즘(Kruskal Algorithm) O(ElogE)
가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘 = 최소 신장 트리를 만들기 위한 알고리즘
그리디 알고리즘(결정의 순간마다 최선의 결정을 함으로써 최종적인 해답에 도달)
간선에 대한 가중치 값이 주어지고 오름차순 한 상태에서 가장 적은거부터 선택하는 것 자체가 그리디
IF) A,B가 가중치가 제일 작아서 이것을 최소 신장 트리에 포함시킨다. 같은 집합에 넣고 싶다. 라는걸 어떻게 구현하면 좋을까?
=> Union - Find
<동작 과정>
1. 최초, 모든 간선을 가중치에 따라 오름차순으로 정렬
2. 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인
2-1) 사이클이 발생하지 않는 경우 최소 신장 트리에 포함(Union)
2-2) 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않는다
3. n-1개의 간선이 선택될 때까지 2를 반복
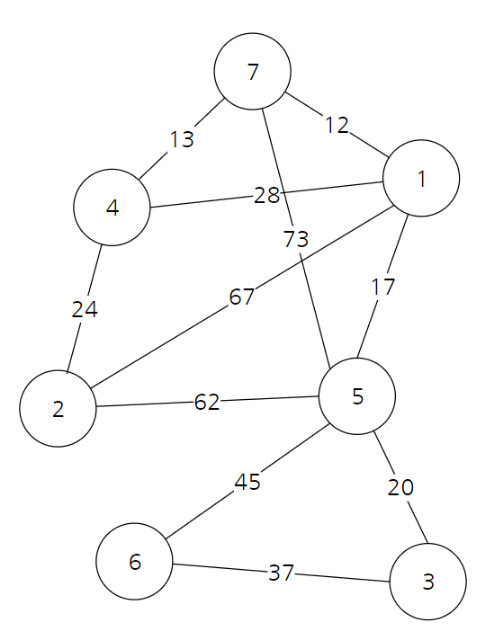
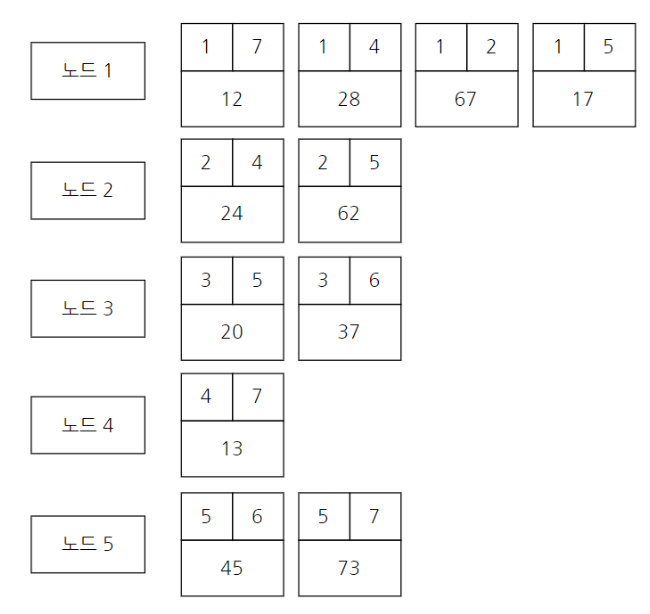
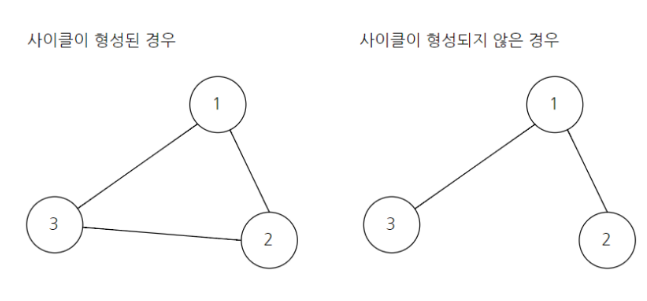
애초에 최소 비용 신장 트리에서는 사이클(같은 집합)이 발생하면 안된다
모든 노드를 이어붙이기만 하면 되는데 사이클이 발생할 이유가 없다
사이클이 발생하는지의 여부는 Union-Find(합집합 찾기) 알고리즘 적용

<연습문제>
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
<Python>
# 특정 원소가 속한 집합을 찾기
def find(parent, x):
if parent[x] == x:
return x
parent[x] = find(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기 (간선 연결한다고 생각!)
def union(parent, a, b):
rootA = find(parent, a)
rootB = find(parent, b)
if rootA < rootB:
parent[rootB] = rootA
else:
parent[rootA] = rootB
import sys
input = sys.stdin.readline
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v + 1)
edges = []
result = 0
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
# 모든 간선에 대한 정보를 입력받기
for _ in range(e):
a, b, cost = map(int, input().split())
# 비용순으로 오름차순 정렬하기 위해 튜플의 첫 번째 원소를 비용으로 설정
edges.append((cost, a, b))
edges.sort()
for edge in edges:
cost, a, b = edge
# 사이클이 발생하지 않는 경우에만 집합에 포함(=연결한다.)
if find(parent, a) != find(parent, b):
union(parent, a, b)
result += cost
print(result)
# sample input
# 7 9
# 1 2 29
# 1 6 75
# 2 3 35
# 2 6 34
# 3 4 7
# 4 6 23
# 4 7 13
# 5 6 53
# 6 7 25<Java>
package practice;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
/* 정점 V의 최대 개수 10,000 => 최대로 나올 수 있는 간선 10^8 / 2
* but, 문제에서 10^5로 제한
* 크루스칼을 쓰는게 좋아보임
* 하지만 프림도 사용가능
*/
public class Main_1197 {
static int V,E;
static int[] parent;
static int[][] data;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
parent = new int[V+1]; //index 1부터 시작하고 싶어서 V+1
data = new int[E][3]; //row : 간선의 수, col : from, to, cost
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < 3; j++) {
data[i][j] = Integer.parseInt(st.nextToken());
}
}
Arrays.sort(data, (o1,o2) -> (o1[2] - o2[2])); //cost에 대해 오름차순
make();
int res = 0;
int cnt = 0;
// 크루스칼 시작
// 오름차순된 간선들을 모두 살펴보면서 그리디 진행
for(int[] row:data) {
if(cnt == V-1)
break;
if (union(row[0],row[1])) {
res += row[2];
cnt++;
}
}
System.out.println(res);
}
public static void make() {
for (int i = 1; i < V+1; i++) {
parent[i] = i;
}
}
//경로 압축해서 표현한 find()
public static int find(int x) {
if (parent[x] != x)
parent[x] = find(parent[x]);
return parent[x];
}
//union
public static boolean union(int x, int y) {
int rootA = find(x);
int rootB = find(y);
//서로의 루트가 같다는건 사이클이 돈다는거니까 false
if (rootA == rootB)
return false;
//서로 다르다면 union을 해주고 true
if (rootA<rootB)
parent[rootB] = rootA;
else
parent[rootA] = rootB;
return true;
}
}'Algorithm > concept' 카테고리의 다른 글
| Coding Test(최단 경로 - Dijkstra, Bellman-Ford, Floyd-Warsahall) (0) | 2022.08.27 |
|---|---|
| Coding Test(Prim Algorithm) (0) | 2022.08.23 |
| Coding Test(Two Pointer) (0) | 2022.06.06 |
| Coding Test(Sliding Window) (0) | 2022.06.06 |
| Coding Test(Union-Find, Disjoint-set) (0) | 2022.05.22 |
